组合数公式

通项公式

$$ \tbinom{n}{m} = \frac{m!}{(m-n)!n!} $$

递推式

三角递推式（适用于求多个组合数）

$$ \tbinom{n}{m} = \tbinom{n}{m-1} + \tbinom{n-1}{m-1} $$

c++代码

void initC(int m)
{
    // C[m][n] 表示 m中选n个
    for (int i = 0; i <= m; i++)
        C[i][0] = 1;
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= i; j++)
            C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}

打表如下

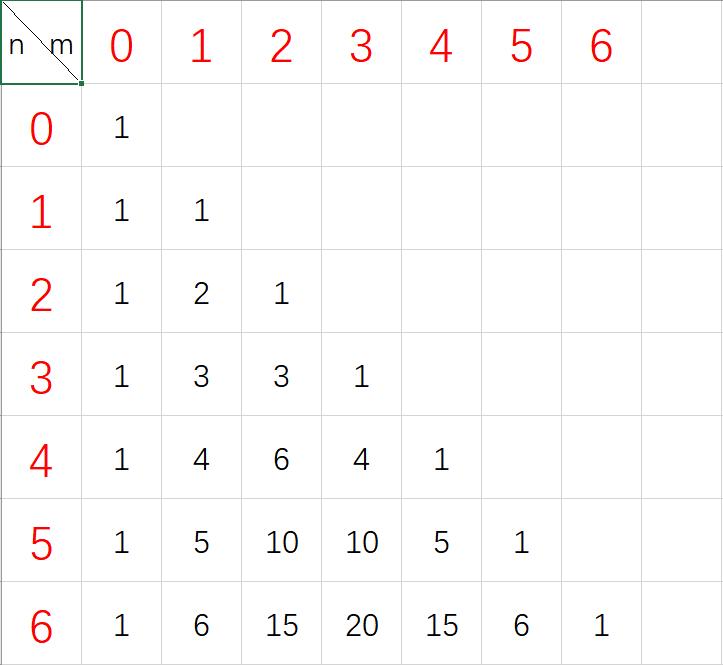
线性递推式（适用于求单个组合数）

$$ \tbinom{n}{m} = \frac{m-n+1}{n} \tbinom{n-1}{m} $$

c++代码

int C(int m, int n) { // 表示 m中选n个
    if (n > m)
        return 0;
    int ans = 1;
    for (int i = 1; i <= n; i++)
        ans = 1LL * ans * (m-i+1) / i;
    return ans;
}

求和公式

公式一

$$ \sum_{i=n}^m \tbinom{n}{i} = \tbinom{n+1}{m+1} $$

可结合三角形递推公式理解

以 $m=4，n=1$ 为例

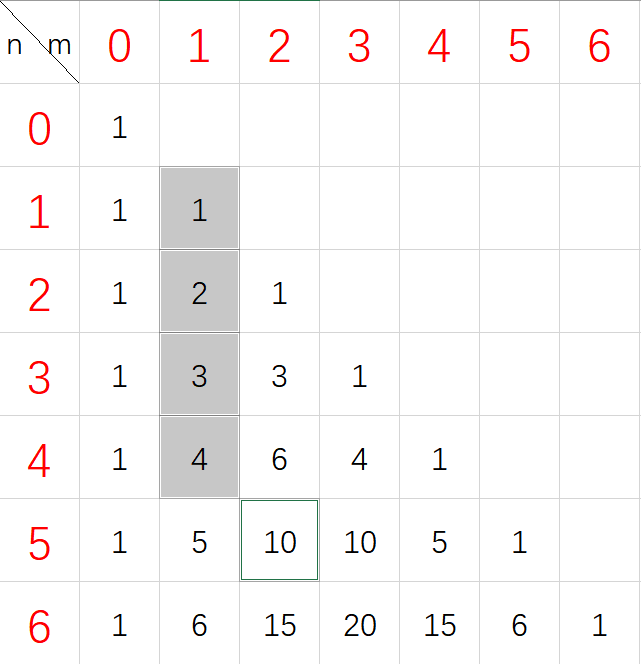
公式二

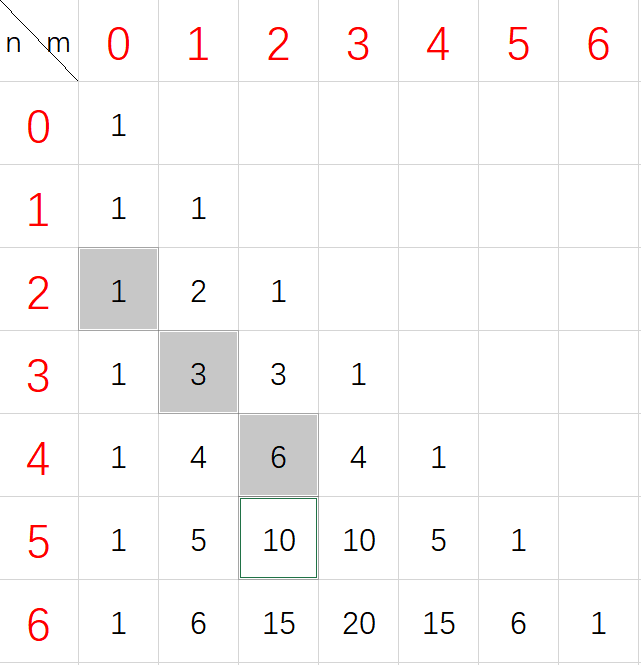
$$ \sum_{i=0}^n \tbinom{i}{i+k} = \tbinom{n}{n+k+1} $$

以 $k=2，n=2$ 为例